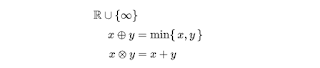The computers like copying the graph, and the center of it has four colours. They pile it until 32291925 vertices. There are five colours. This is called the Hadwiger-Nelson problem. You need to choose the minimum value.
This is the graph H, which is the center of the expansion. There are 4 colours. The center is yellow, but the distance of 1 must be the different colours.
This is the graph J, which contains 31 vertices and 13 copies of H.
Then you change the color.
This is different from J. The center is H, and there are 6 copies of H. The distance from the center is √3.
Moreover, black vertices are included, so they are different hexagons from H. There is no same one.
There are 7 hexagons. This chromatic number is 7.
This is the graph K, which has 61 vertices. This is 2 copies of J.
This is the graph L, which has 121 vertices. This is 2 copies of K.
This is M which has 20425 vertices.
This is G which has 32291925 vertices. This is very complicated and highly dense. Therefore, it is hard to find the four coloured core in recent computing.
You remember that this is the center of G, so there must be 5 colours. The distance of black vertices is 1, but they can assume any colour so long as no connected vertices are the same colour.
2018年7月24日火曜日
2018年5月9日水曜日
Tropical Geometry
What is tropical geometry?
EX1.
K is algebraic closure, and V is closed manifold.
This is the tropical manifold.
EX2.
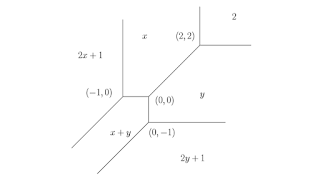
6x^2→2x+1, 5xy→x+y, 10y^2→2y+1, 3x→x, -y→ y, 4→2
EX1.
K is algebraic closure, and V is closed manifold.
This is the tropical manifold.
EX2.
6x^2→2x+1, 5xy→x+y, 10y^2→2y+1, 3x→x, -y→ y, 4→2
2018年5月7日月曜日
Homological algebra for abelian categories
This is the development of a cohomological theory. You may call it tropical geometry.
EX.
You see P^3→P^2, so this seems to be fractal.
Bmod is the replacement for the category of abelian groups.
C admits equalizers Equ and coequalizers Coequ.
This is the natural morphism.
EX.
You see P^3→P^2, so this seems to be fractal.
Bmod is the replacement for the category of abelian groups.
For all a, b in A, a • b = b • a
C admits equalizers Equ and coequalizers Coequ.
This is the natural morphism.
2018年4月23日月曜日
The Sylvester-Gallai Theorem
The deformation is the mathematical concept.
The Sylvester-Gallai Theorem is that a finite set of points in the plane have the proper line through any two of them, and it passes through a third point of the set. Moreover, it must be on the same line.
P is the the noncollinear finite set. S(P) is the set of connecting lines in P.
p and s are perpendicular, so they are not the ordinary line. (s*,p*) is the smallest distance, and s* is in the ordinary line.
l must be the ordinary line. This is the contradiction.
There is the cyclically intersection points (p,x1).
x1,・・・xk is on l. Moreover it crosses S. This must be ordinary.
You also see the extra dimensions.
i lines are determined by P.
The Sylvester-Gallai Theorem is that a finite set of points in the plane have the proper line through any two of them, and it passes through a third point of the set. Moreover, it must be on the same line.
P is the the noncollinear finite set. S(P) is the set of connecting lines in P.
p∈P, s∈S(P)
p and s are perpendicular, so they are not the ordinary line. (s*,p*) is the smallest distance, and s* is in the ordinary line.
l∩P={p}
l must be the ordinary line. This is the contradiction.
l∩S(P)
There is the cyclically intersection points (p,x1).
x1,・・・xk is on l. Moreover it crosses S. This must be ordinary.
You also see the extra dimensions.
i lines are determined by P.
2018年3月24日土曜日
Deformations
This is the last conjecture of Stephen Hawking. You need the singularity to exceed his theory. This is the the holographic no-boundary wave function.
(hij, φ) is the wave function, and S is the usual surface terms. Z is the Euclidean AdS/CFT.
The black birds move to the infinite on the surface without directions. Moreover, this is like a cylinder. Euclidean AdS/CFT generalized to complex relevant deformations implies an approximate realisation.
This is the mass deformed free model partition function, and m^2 is supergravity theories which typically contain scalars of mass.
This is the action of the free O(N) model, and O(N) is the partition function of supersymmetry breaking deformations.
You plot two one-dimensional slices of the distribution for two different values of ~m^2.
①
~m^2=0
②
~m^2=0.05i
This conjecture strengthens the intuition that holographic cosmology implies a significant reduction of the multiverse to a much more limited set of possible universes.
(hij, φ) is the wave function, and S is the usual surface terms. Z is the Euclidean AdS/CFT.
The black birds move to the infinite on the surface without directions. Moreover, this is like a cylinder. Euclidean AdS/CFT generalized to complex relevant deformations implies an approximate realisation.
This is the mass deformed free model partition function, and m^2 is supergravity theories which typically contain scalars of mass.
This is the action of the free O(N) model, and O(N) is the partition function of supersymmetry breaking deformations.
You plot two one-dimensional slices of the distribution for two different values of ~m^2.
①
~m^2=0
②
~m^2=0.05i
This conjecture strengthens the intuition that holographic cosmology implies a significant reduction of the multiverse to a much more limited set of possible universes.
2018年3月20日火曜日
1+2+3+4+・・・
This is irrational because this must increase infinitely basically.
This is like a black hole.
Srinivasa Aiyangar Ramanujan solved it.
2F=1
∴F=1/2
∴
A=1/4
∴
S=-1/12
This is tricky in infinity because he moves the series.
You can also use the Zeta Function.
This is A=1-2+3-4+・・=1/4
This is the Abel's summability method.
This is F=1-1+1-1+・・・=1/2
∴
ζ(-1)=1+2+3+4+・・・=-1/12
2018年3月2日金曜日
Whole Genome Shotgun Sequencing
This is the Hamiltonian path problem, which is closed.
V(G)={a,b,c,d,e,f,g,h}
This is the graph of each dot.
E(G)={ab,bc,cd,de,ef,fg,gh,ha}
This is the graph of the Hamiltonian path.
Then you see the Whole Genome Shotgun Sequencing.
This isn't closed, but there is the Hamiltonian path.
S4→S2→S1→S3→S5
You cut the chain of your DNA, and you reorganize it.
S1→ACCTG
S2→CGACC
S3→CTGAG
S4→CGTCG
S5→AGTAC
∴
S4→CGTCG
S2→XXXCGACC
S1→XXXXXACCTG
S3→XXXXXXXCTGAG
S5→XXXXXXXXXXAGTAC
You connect the pattern.
CGTCGACCTGAGTAC
登録:
投稿 (Atom)