2018年11月28日水曜日
Penrose tiling
Penrose tiling is based on Golden Ratio (a=φ:b=1), but you can't use this rhombus because of aperiodicity.
{a: Kite}
{b: Dart}
You connect these Kite and Dart randomly. Then you see tiling like these.
This is like the Maurits Cornelis Escher's painting, but it is periodic.
2018年11月5日月曜日
Farey sequence
F(1) | 0/1 | 1/1 | |||||||||
F(2) | 0/1 | 1/2 | 1/1 | ||||||||
F(3) | 0/1 | 1/3 | 1/2 | 2/3 | 1/1 | ||||||
F(4) | 0/1 | 1/4 | 1/3 | 1/2 | 2/3 | 3/4 | 1/1 | ||||
F(5) | 0/1 | 1/5 | 1/4 | 1/3 | 2/5 | 1/2 | 3/5 | 2/3 | 3/4 | 4/5 | 1/1 |
(φ(n)=Euler's totient function)
φ(n) is the sum of numbers which are non divisors of n. You ignore 1.
ex.
φ(12)= 4 ⇒ (1,5,7,11)
φ(13)=12 ⇒ (1,2,3,4,5,6,7,8,9,10,11,12)
φ(14)= 6 ⇒ (1,3,5,9,11,13)
Farey sequence is related to Ford circle.
F(n+1)=(p+r)/(q+s)
You see F(2). 1/2=(0/1)+(1/1)
In F(3), 1/3=(0/1)+(1/2) and 2/3=(1/2)+(1/1)
In F(4), 1/4=(0/1)+(1/3) and 3/4=(2/3)+(1/1)
In F(5), φ(5)=4. 1/5=(0/1)+(1/4), 2/5=(1/3)+(1/2), 3/5=(1/2)+(2/3), 4/5=(3/4)+(1/1)
2018年11月3日土曜日
Ford circle
Ford circle is based on Golden Ratio.
These circles are tangent.
C(p/q), C(r/s), C((r-p)/(s-q))=C(1/0)
∴
ps-qr=±1
Then, you see that circles are the convergence.
τ is the Golden Ratio.
You also think about irrational numbers (ω), and this is zero (∞)=C(1/0).
2018年10月31日水曜日
Sphere Packing
You need to fill spheres in packing infinitely. This is more complicated than packing oranges.
Two dimensions are easy to image, but spheres are three dimensions and you pile them infinitely.
This is n-dimensional Pythagorean theorem, the distance between (a,b,c,d) and (w,x,y,z) in R^n.
There are always spaces between spheres. You need to put small ones. Fraction of boundary is less than 0.99. You can find 99% spaces for spheres anytime.
∴
0.99^300≒0.049
0.99^500≒0.00657
0.99^800≒0.00032
Therefore, spheres are almost zero in higher dimensions.
Two dimensions are easy to image, but spheres are three dimensions and you pile them infinitely.
This is n-dimensional Pythagorean theorem, the distance between (a,b,c,d) and (w,x,y,z) in R^n.
There are always spaces between spheres. You need to put small ones. Fraction of boundary is less than 0.99. You can find 99% spaces for spheres anytime.
∴
0.99^n
0.99^300≒0.049
0.99^500≒0.00657
0.99^800≒0.00032
Therefore, spheres are almost zero in higher dimensions.
2018年8月22日水曜日
Four Color Theorem
You need just four colors to fill any realms in your flat spaces. This is called Four color theorem.
You prove it by induction.
At first, there are 3 countries in your map. You can add the one color.
There is the rule which must be the different color when they face each other. Therefore, yellow is acceptable.
Then, you have 4 countries in your map. Do you need 5 colors to fill your space?
This is complicated, and you need to choose the color to adjust the Four color theorem.
You don't need 5 colors.
Is this induction satisfied with any situation?
This is beyond our ability. The Four color theorem seems to be correct, but we rely on the computer.
You prove it by induction.
At first, there are 3 countries in your map. You can add the one color.
There is the rule which must be the different color when they face each other. Therefore, yellow is acceptable.
Then, you have 4 countries in your map. Do you need 5 colors to fill your space?
This is complicated, and you need to choose the color to adjust the Four color theorem.
You don't need 5 colors.
Is this induction satisfied with any situation?
This is beyond our ability. The Four color theorem seems to be correct, but we rely on the computer.
2018年7月24日火曜日
The Hadwiger-Nelson Problem
The computers like copying the graph, and the center of it has four colours. They pile it until 32291925 vertices. There are five colours. This is called the Hadwiger-Nelson problem. You need to choose the minimum value.
This is the graph H, which is the center of the expansion. There are 4 colours. The center is yellow, but the distance of 1 must be the different colours.
This is the graph J, which contains 31 vertices and 13 copies of H.
Then you change the color.
This is different from J. The center is H, and there are 6 copies of H. The distance from the center is √3.
Moreover, black vertices are included, so they are different hexagons from H. There is no same one.
There are 7 hexagons. This chromatic number is 7.
This is the graph K, which has 61 vertices. This is 2 copies of J.
This is the graph L, which has 121 vertices. This is 2 copies of K.
This is M which has 20425 vertices.
This is G which has 32291925 vertices. This is very complicated and highly dense. Therefore, it is hard to find the four coloured core in recent computing.
You remember that this is the center of G, so there must be 5 colours. The distance of black vertices is 1, but they can assume any colour so long as no connected vertices are the same colour.
This is the graph H, which is the center of the expansion. There are 4 colours. The center is yellow, but the distance of 1 must be the different colours.
This is the graph J, which contains 31 vertices and 13 copies of H.
Then you change the color.
This is different from J. The center is H, and there are 6 copies of H. The distance from the center is √3.
Moreover, black vertices are included, so they are different hexagons from H. There is no same one.
There are 7 hexagons. This chromatic number is 7.
This is the graph K, which has 61 vertices. This is 2 copies of J.
This is the graph L, which has 121 vertices. This is 2 copies of K.
This is M which has 20425 vertices.
This is G which has 32291925 vertices. This is very complicated and highly dense. Therefore, it is hard to find the four coloured core in recent computing.
You remember that this is the center of G, so there must be 5 colours. The distance of black vertices is 1, but they can assume any colour so long as no connected vertices are the same colour.
2018年5月9日水曜日
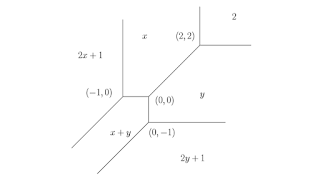
Tropical Geometry
What is tropical geometry?
EX1.
K is algebraic closure, and V is closed manifold.
This is the tropical manifold.
EX2.
6x^2→2x+1, 5xy→x+y, 10y^2→2y+1, 3x→x, -y→ y, 4→2
EX1.
K is algebraic closure, and V is closed manifold.
This is the tropical manifold.
EX2.
6x^2→2x+1, 5xy→x+y, 10y^2→2y+1, 3x→x, -y→ y, 4→2
登録:
コメント (Atom)