B0
B0*2C0
B0*3C0+B1*3C1
B0*4C0+B1*4C1+B2*4C2
B0*5C0+B1*5C1+B2*5C2+B3*5C3
B0*6C0+B1*6C1+B2*6C2+B3*6C3+B4*6C4
B0*7C0+B1*7C1+B2*7C2+B3*7C3+B4*7C4+B5*7C5
| 1 | |||||
| 1 | 3 | ||||
| 1 | 4 | 6 | |||
| 1 | 5 | 10 | 10 | ||
| 1 | 6 | 15 | 20 | 15 | |
| 1 | 7 | 21 | 35 | 35 | 21 |
| B0 | B1 | B2 | B3 | B4 | B5 |
B0=1, B1=-1/2 but 1/2, B2=1/6, B3=0, B4=-1/30, B5=0
Now I see Bernoulli numbers in the Samurai era, although the country has been closed except for Holland and Portugal. We never know it in those days. Some Europeans may have taught us.
B6=1/42.
I clearly see it.
We don't understand the reason, but it seems to be Pascal's triangle. N=6 and K=4
5C3=10
Then this samurai multiplies Bernoulli numbers apparently. You sum the line between 1 and 0.
EX.
3/2+1/2=2
2+1=3
5/2+5/3-1/6=4
3+5/2-1/2=5
7/2+7/2-7/6+1/6=6
4+14/3-7/3+2/3=7
9/2+6-21/5+2-3/10=8
5+15/2-7+5-3/2=9
11/2+55/6-11+11-11/2+5/6=10
6+11-33/2+22-33/2+5=11
You get 1 to 11. This is compression, and I try to find B12. (13/2)+13+0-(143/6)+0+(286/7)+0-(429/10)+0+(65/3)+0+13B12=12
B12=-691/2730


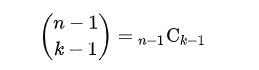




0 件のコメント:
コメントを投稿