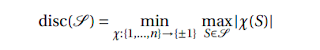Fibonacci number

F is Fibonacci number. Fm divide Fn, and m divide n.

F2=F0+F1=0+1=1

F3=F1+F2=1+1=2

F4=F2+F3=1+2=3

n=3m → F(2,8,34,144,610,2584,10946,・・・)

∴ Fm=F3=2

n=4m → F(3,21,144,987,6765,・・・)

∴ Fm=F4=3

n=5m → F(5,55,610,6765,・・・）

∴ Fm=F5=5

This is fractal and expansion.

The Boltzmann fair division for distributive justice

You have a cake, and there are three people. You need to divide it fair. ⅓ and 120° are the good choices. This is an easy one, which is 1/n in n people. Our society is more complicated. The demand of the cake is required by your ability and contribution. This is often greedy and competitive. The Boltzmann distribution is based on entropy maximization and provides the most probable, natural, and unbiased distribution of a physical system.

Ej is the division potential, and j is players.

β is a division constant. (β≧0)

When β is Zero, all players receive an equal amount of cake. When β increases to a large value, only a few players having made the highest cake contributions receive most of the cake.

The player’s need for the cake as the need values Dj satisfy: uj(0) = 0, uj(Dj) = tanh(1)≅ 0.762. This means that if a player receives what they need (Dj), they satisfy 76.2%.

Homogeneous cake cutting is the total number of cake units, Ej is the division potential of player j, and Pj is the Boltzmann probability that a cake unit is allocated to player j.

Heterogeneous cake cutting is the total number of cake units with flavor i which is the weight factor expressing player j’s preference for flavor i, and the Boltzmann probability that a cake unit of flavor i is allocated to player j.

In β≧0.029,equality starts decreasing.

Discrepancy theory

There is a finite set of elements {1,2,・・n}.

S1,...,Sm ⊆ {1,...,n}

There are two colors.

S={{い,ろ,は},{い,に},{に,ほ},{は,ほ}}

∴

This is the discrepancy.

Then you see the binary distribution.

You see -1={{い,ろ,は}{い,に}{に,ほ}} and 1={は,ほ}. This is at most 50%.

B-tree

Every node has at most m children, and every node has at least m/2 children. This is known as binary.

This is the maximum number of potential search keys for each node in a B-tree.

4 is the maximum, so you have the root.

This is expansion. Therefore, your computer need to optimize your huge data.

This is back and forth.

Stochastic block model

Stochastic block model is random graphs which contain communities, subsets of nodes. There are n vertices and disjoint subsets C1・・・Cr. C is a community. P is a symmetric matrix with edge probabilities.

G(n,M)

Thi is the Erdős–Rényi random graph model which have n nodes and M edges.

G(3,2)

G(n,p)

You have more vertices. It is almost Zero.

Tschirnhaus transformation

Tschirnhaus transformation is a polynomial equation of degree (n≧2) with some nonzero intermediate coefficients.

-------------------------------------------------------------------------------------------------------

Ex.
n=3

a’1=0 and a’2=0

-------------------------------------------------------------------------------------------------------

K is a field, and P(t) is polynomial over K.

K(t)/P(t)=L

L=K(α)

α is t modulo P.

β=F(α), α=G(β)

F and G over K are polynomials. Moreover, Q is the minimal polynomial for β over K. This is the Tschirnhaus transformation of P.

L is a Galois extension of K.

Huffman coding

In your fractal data, you can compress the huge chain. It depends on frequency of occurrence, so if you use more, you can shorten the code.

You have BACE. This is 001000010100 which is 4*3=12 bits. You put A is 0 and B is 1. BACE is 10010100. This is 8 bits which is about 67% compression. MP3 and JPEG are well known.

This is the information content h (in bits) of each symbol ai with non-null probability, which are binary.

The entropy H (in bits) is the weighted sum, across all symbols ai with non-zero probability wi, of the information content of each symbol.

Jordan normal form

This is a square matrix.

A is the algebraically closed field. In mathematics, a field F is algebraically closed if every non-constant polynomial in F[x] has a root in F. Moreover, P is the regular matrix. J is called Jordan normal form.

Ae1=5e1

Ae2=e1+5e2

Ae3=e2+5e3

You can write this.

A5e1=0

A5e2=e1

A5e3=e2

∴
e3→e2→e1→0

e is an eigenvector of A.

This is called Computational Topology.

1-2-3 Conjecture

1-2-3 Conjecture is a graph G = (V, E). It is is simple, finite, and undirected. You see the triangle. This is ∅=0.

u,v∈V(G)

u and v are any adjacent vertices. The sum of weights of edges incident to u differs from the sum of weights of edges incident to v. Then, the edges of G may be assigned weights from the set {1, 2, 3}. This is 1-2-3 Conjecture. You can color the proper vertexes.

Bernoulli Differential Equations

Higher dimensions are x^n. It is hard to capture more than 4 dimensions. It may be religion. I have studied Zen in English, but I often see words like emptiness, nothingness and absurdity.

Bernoulli Differential Equations apply chain rule to integrate this complicated differences.

This is a linear differential equation.

Hyperplane separation theorem

Misunderstanding is crucial, when their connection is empty. This abstract algebra is called Krull's separation lemma.

I∩M=∅

I is ideal, and M is multiplicative and closed.

P is the prime ideals for the integers that contain all the multiples of a given prime number, together with the zero ideal.

I⊆P

P∩M=∅

This is disjoint convex sets in higher dimensional Euclidean space. A and B are disjoint nonempty convex subsets.

[x,v]≧c and [y,v]≦c

v is a nonzero vector, and c is a real number. x is in A, and y is in B. If both sets are closed, and at least one of them is compact, then the separation can be strict. This is called Hyperplane separation theorem.

Pólya conjecture

10=2*5 There are 2 prime numbers which are called prime factorization.

This is n=50.

4=2^2 is 2 prime numbers.

12=2^2*3 is 3 prime numbers.

I put even numbers in 1. There are 21 in 50. According to Pólya conjecture, there are more odd numbers in prime factorization.

Prime numbers are chaotic, so this conjecture isn't fractal like piling squares.

906,150,257 ≤ n ≤ 906,488,079

There are more even numbers in n.

It is hard to put circles in the square. I think that you need to adjust the range of the square to extinguish the circle, such as 906000000≦n≦906500000.

For example, there are 7 even numbers in 4≦n≦16. This is contradictory.

Wolstenholme's theorem

p is a prime number (p≧5).

When p is 5, p^3=125.

2376 is one more than a multiple of 125. 2376=125*19+1

When p is 7, p^3=343.

1716 is one more than a multiple of 343.

This is chaotic, but you can find it by your spreadsheet.

Moreover, this is Binomial coefficient. Pascal's triangle is well known as fractal.

This is harmonic numbers.

You see that this is almost zeta function.

Riemann's zeta function is ζ(s)=0.