∴0!=1
2022年12月29日木曜日
Gamma function
This is gamma function.
Z include complex numbers. Z>0
Then, you see Riemann zeta function.
You can also write this.
You can get 1 finally.
2022年12月23日金曜日
Fractional Calculus
Irrationality is a philosophical question. Now we talk about AI, but the computational world often avoids this problem. If D is prime numbers, this square root of D is irrational. When you have 100=10*10, 10 is not the prime numbers. 7 is the biggest prime number in 10. The square root of 7 is irrational. 2,3,5,7 are prime numbers in 100. Then you expand integers eternally. I define that this is fractal.
This is called Cauchy’s formula for repeated integration. The generalization of the factorial function is the gamma function.
This is the left Riemann-Liouville integral. α is complex and greater than zero. The special case of α = 1/2 is called the semi-integral.
The gamma function is not defined for zero or for negative integers.
This is irrational.
This is the left Riemann-Liouville fractional derivative.
The Riemann-Liouville differintegral continuously transforms between the functions f(x) = x, f(x) = 1, and f(x) = (1/2)x^2, and α ranging from -1 to 1.
This is waving.
2021年9月27日月曜日
Homotopy group
Spotify is the famous viral media. Your MP3 file spread all over the world qickly because of the internet, although you need to be famous. We have different divices to listen our favorite music. This is addiction and virus actually. Their industry is huge, and Apple is popular.
This is vaccinated because of math. There is no rock star but logic.
You have a sphere which is the earth. You can use iPhone anywhere because of the universal network like Starlink.
Then you have a doughnut in Starbucks.
You can eat it, but you are not there. Starbucks isn't the doughnut. They are the different group. This is homotopy. The doughnut is called torus.
T is torus, and C is the complex plane.
∴
S is the earth. Therefore, this isn't real.
Moreover, This is metric.
This is the maxium range.
H is homotopy.
However, when you have your CD, you need to buy it and have MP3. This is time which is the different dimension. You can't put your music on the web directly.
This is false.
This is vaccinated because of math. There is no rock star but logic.
You have a sphere which is the earth. You can use iPhone anywhere because of the universal network like Starlink.
Then you have a doughnut in Starbucks.
You can eat it, but you are not there. Starbucks isn't the doughnut. They are the different group. This is homotopy. The doughnut is called torus.
T is torus, and C is the complex plane.
∴
S is the earth. Therefore, this isn't real.
Moreover, This is metric.
w(f)∈Z
w(f)=w(g)
∥f∥=sup(|f|)
This is the maxium range.
∥f∥≦L and ∥g∥≦L
∥H∥≦L
H is homotopy.
However, when you have your CD, you need to buy it and have MP3. This is time which is the different dimension. You can't put your music on the web directly.
This is false.
2021年7月11日日曜日
Collatz problem
2 is the only even prime number. Moreover, prime numbers are fractal.
Collatz problem is divided by two parts which are even and odd numbers. When you have odd numbers, you put them in 3n+1. Then you always have even numbers, so you divide them by 2.
You repeat it over and over again, until you get 1. At first, you have odd numbers (3-29). You put them in 3n+1. You see (10,16,22・・・,88). You divide them by 2 such as (5,8,11・・,44). Half of them are odd numbers which are yellow. The others are even numbers, so you keep dividing them by 2 such as (4,7,10,13,16,19,22). Green numbers are odd which is 50%. This is fractal. You see 1 in the end.
Ex.
●17-52-26-13-40-20-10-5-16-8-4-2-1
●25-76-38-19-58-29-88-44-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1
●65-196-98-49-148-74-37-112-56-28-14-7-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1
This is expansion and still fractal.
Ex.
●133-400-200-100-50-25-76-38-19-58-29-88-44-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1
Collatz problem is divided by two parts which are even and odd numbers. When you have odd numbers, you put them in 3n+1. Then you always have even numbers, so you divide them by 2.
You repeat it over and over again, until you get 1. At first, you have odd numbers (3-29). You put them in 3n+1. You see (10,16,22・・・,88). You divide them by 2 such as (5,8,11・・,44). Half of them are odd numbers which are yellow. The others are even numbers, so you keep dividing them by 2 such as (4,7,10,13,16,19,22). Green numbers are odd which is 50%. This is fractal. You see 1 in the end.
Ex.
●17-52-26-13-40-20-10-5-16-8-4-2-1
●25-76-38-19-58-29-88-44-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1
●65-196-98-49-148-74-37-112-56-28-14-7-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1
This is expansion and still fractal.
Ex.
●133-400-200-100-50-25-76-38-19-58-29-88-44-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1
2021年7月8日木曜日
Hodge conjecture
Hodge conjecture is the algebraic topology of a non-singular complex algebraic variety. Therefore, elliptic curves should be correlated with it because of the rational point.
X is a compact complex manifold of complex dimension n. Moreover, its cohomology groups lie in degrees zero through 2n. Elliptic curves are the two dimensions, although you pile them in Riemann sphere. There must be a decomposition on its cohomology with complex coefficients.
(p,q) is harmonic forms. These are the cohomology classes represented by differential forms such as Z1,...,Zn.
Z is a complex submanifold of X.
α is integration.
You can also write this.
i:Z→X
α is integration.
You can also write this.
2021年4月14日水曜日
Complex multiplication
Elliptic curves have an endomorphism ring larger than the integers, which are higher dimensions of abelian varieties.
C is complex multiplication, and Z[i] is the Gaussian integer ring, and θ is any non-zero complex number.
You can see always the Gaussian integer as module in Elliptic curves.
59 is the Gaussian prime.
The Gaussian prime must be symmetry in any Elliptic curves.
2=(1-i)(1+i)=(-1-i)(-1+i)
This is the norm. 1±i,-1±i are Gaussian primes.
±3,±3i,5=(2-i)(2+i)=(1-2i)(1+2i),±7,±7i,13=(2+3i)(2-3i)=(3+2i)(3-2i),17=(4-i)(4+i)=(1+4i)(1-4i)
59 is the Gaussian prime.
I think that it is fractal.
C/ΘZ[i]
C is complex multiplication, and Z[i] is the Gaussian integer ring, and θ is any non-zero complex number.
You can see always the Gaussian integer as module in Elliptic curves.
Y^2=X^3-X+1
59 is the Gaussian prime.
The Gaussian prime must be symmetry in any Elliptic curves.
2=(1-i)(1+i)=(-1-i)(-1+i)
This is the norm. 1±i,-1±i are Gaussian primes.
±3,±3i,5=(2-i)(2+i)=(1-2i)(1+2i),±7,±7i,13=(2+3i)(2-3i)=(3+2i)(3-2i),17=(4-i)(4+i)=(1+4i)(1-4i)
Y^2=4X^3-X
59 is the Gaussian prime.
I think that it is fractal.
2021年4月3日土曜日
Gaussian primes
This is quite tricky. Modulo primes in Y^2=X^3-X are sometimes primes.
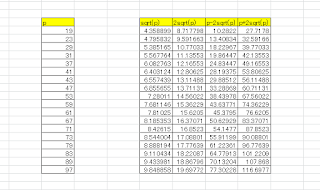
p is prime, and sqrt is √
When p is 19, N is 19.
p=23 - N=23
p=29 - N=39
Carl Friedrich Gauss proved it. Moreover, p=N is Gaussian primes such as 19 and 23. This is Gaussian integers which are complex numbers. Elliptic curve is rational, so this is contradictory but prime is real. 5=(2+i)(2-i)
You can divide 5 in Z[i], so 5 isn't prime. However, 5 is prime in the real world.
This is Fermat's theorem on sums of two squares.
ex. 5,13=(2+3i)(2-3i),17=(1+4i)(1-4i),29=(2+5i)(2-5i)
When 3=αβ, this isn't also prime in Z[i].
N is the norm.
N(a+bi):=a^2+b^2=(a+bi)(a-bi)
N(αβ)=N(α)N(β)
3≠(a+bi)(a-bi)
Therefore, 3 is prime in Z[i].
4n+3 is Gaussian primes such as 3,7,11,19,23,31,43,47,59,67,71,79,83. This is in Y^2=X^3-X.
E(N) is the sum of the same modules in Y^2=X^3-X. G(p) is Gaussian primes.
You see COUNTIF(mod(y^2),mod(x^3-x)) which is p=N.
python
p-2sqrt(p) < N < p+2sqrt(p)
p is prime, and sqrt is √
When p is 19, N is 19.
p=23 - N=23
p=29 - N=39
Carl Friedrich Gauss proved it. Moreover, p=N is Gaussian primes such as 19 and 23. This is Gaussian integers which are complex numbers. Elliptic curve is rational, so this is contradictory but prime is real. 5=(2+i)(2-i)
You can divide 5 in Z[i], so 5 isn't prime. However, 5 is prime in the real world.
This is Fermat's theorem on sums of two squares.
p≡1 (mod 4)
ex. 5,13=(2+3i)(2-3i),17=(1+4i)(1-4i),29=(2+5i)(2-5i)
When 3=αβ, this isn't also prime in Z[i].
N is the norm.
N(a+bi):=a^2+b^2=(a+bi)(a-bi)
N(αβ)=N(α)N(β)
3≠(a+bi)(a-bi)
Therefore, 3 is prime in Z[i].
4n+3 is Gaussian primes such as 3,7,11,19,23,31,43,47,59,67,71,79,83. This is in Y^2=X^3-X.
E(N)=G(p)≒4n+3≠(a+bi)(a-bi)
E(N) is the sum of the same modules in Y^2=X^3-X. G(p) is Gaussian primes.
You see COUNTIF(mod(y^2),mod(x^3-x)) which is p=N.
python
登録:
投稿 (Atom)