The Birch and Swinnerton-Dyer Conjecture

This is the Birch and Swinnerton-Dyer Conjecture. Np is the number of points on E which is an elliptic curve over Q. 【mod p】 is on E, and p is a prime. If the rank of E is large then on average E should have more than p points. This is X. c is constant.

Q is rational numbers.

At first, you see a circle. X^2+y^2=1

P is a rational point. You have a line (-1,0) to P. s is a slope.

Y=s(X+1)

Then you put the line to X^2+y^2=1.

(s^2+1)X^2+(2s^2)X+(s^2-1)=0

∴ X=-1, (1-s^2)/(1+s^2)

You see P on the line.

P is a rational point on π, so it is infinite.

Q∪｛∞｝

If f(X,Y)=0, you pile circles and you have the point of infinity.

C is complex plane. P(C) is Riemann sphere.

This is the point of infinity. This cone is the three dimensions. This is quite complicated because of no rational point. Then you use an elliptic curve.

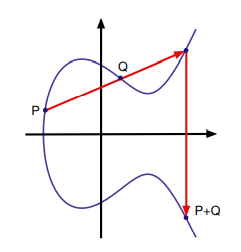
You can ignore zero.

P and Q are rational points, so P+Q on E is still rational even if P+Q is the point of infinity.

T is some finite abelian group.