Homotopy group

Spotify is the famous viral media. Your MP3 file spread all over the world qickly because of the internet, although you need to be famous. We have different divices to listen our favorite music. This is addiction and virus actually. Their industry is huge, and Apple is popular.

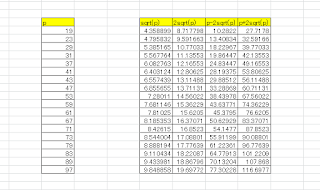
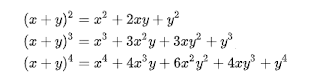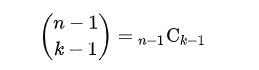This is vaccinated because of math. There is no rock star but logic.

You have a sphere which is the earth. You can use iPhone anywhere because of the universal network like Starlink.

Then you have a doughnut in Starbucks.

You can eat it, but you are not there. Starbucks isn't the doughnut. They are the different group. This is homotopy. The doughnut is called torus.

T is torus, and C is the complex plane.

∴

S is the earth. Therefore, this isn't real.

Moreover, This is metric.

w(f)∈Z

w(f)=w(g)

∥f∥=sup(｜f｜)

This is the maxium range.

∥f∥≦L and ∥g∥≦L

∥H∥≦L

H is homotopy.

However, when you have your CD, you need to buy it and have MP3. This is time which is the different dimension. You can't put your music on the web directly.

This is false.

Collatz problem

2 is the only even prime number. Moreover, prime numbers are fractal.

Collatz problem is divided by two parts which are even and odd numbers. When you have odd numbers, you put them in 3n+1. Then you always have even numbers, so you divide them by 2.

You repeat it over and over again, until you get 1.

At first, you have odd numbers (3-29). You put them in 3n+1. You see (10,16,22・・・,88). You divide them by 2 such as (5,8,11・・,44). Half of them are odd numbers which are yellow. The others are even numbers, so you keep dividing them by 2 such as (4,7,10,13,16,19,22). Green numbers are odd which is 50%. This is fractal. You see 1 in the end.

Ex.
●17-52-26-13-40-20-10-5-16-8-4-2-1

●25-76-38-19-58-29-88-44-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1

●65-196-98-49-148-74-37-112-56-28-14-7-22-11-34-17-52-26-13-40-20-10-5-16-8-4-2-1

Hodge conjecture

Hodge conjecture is the algebraic topology of a non-singular complex algebraic variety. Therefore, elliptic curves should be correlated with it because of the rational point.

X is a compact complex manifold of complex dimension n. Moreover, its cohomology groups lie in degrees zero through 2n. Elliptic curves are the two dimensions, although you pile them in Riemann sphere. There must be a decomposition on its cohomology with complex coefficients. (p,q) is harmonic forms. These are the cohomology classes represented by differential forms such as Z1,...,Zn.

Z is a complex submanifold of X.

i:Z→X

α is integration.

You can also write this.

Complex multiplication

Elliptic curves have an endomorphism ring larger than the integers, which are higher dimensions of abelian varieties.

C/ΘZ[i]

C is complex multiplication, and Z[i] is the Gaussian integer ring, and θ is any non-zero complex number.

You can see always the Gaussian integer as module in Elliptic curves.

---

Y^2=X^3-X+1

59 is the Gaussian prime.

---

The Gaussian prime must be symmetry in any Elliptic curves.

2=(1-i)(1+i)=(-1-i)(-1+i)

This is the norm. 1±i,-1±i are Gaussian primes.

±3,±3i,5=(2-i)(2+i)=(1-2i)(1+2i),±7,±7i,13=(2+3i)(2-3i)=(3+2i)(3-2i),17=(4-i)(4+i)=(1+4i)(1-4i)

---

Y^2=4X^3-X

59 is the Gaussian prime.

---

I think that it is fractal.

Gaussian primes

This is quite tricky. Modulo primes in Y^2=X^3-X are sometimes primes.

p-2sqrt(p) < N < p+2sqrt(p)

p is prime, and sqrt is √

When p is 19, N is 19.
p=23 - N=23
p=29 - N=39

Carl Friedrich Gauss proved it. Moreover, p=N is Gaussian primes such as 19 and 23.

This is Gaussian integers which are complex numbers. Elliptic curve is rational, so this is contradictory but prime is real.

5=(2+i)(2-i)

You can divide 5 in Z[i], so 5 isn't prime. However, 5 is prime in the real world.

This is Fermat's theorem on sums of two squares.

p≡1 (mod 4)

ex. 5,13=(2+3i)(2-3i),17=(1+4i)(1-4i),29=(2+5i)(2-5i)

When 3=αβ, this isn't also prime in Z[i].

N is the norm.

N(a+bi):=a^2+b^2=(a+bi)(a-bi)
N(αβ)=N(α)N(β)

3≠(a+bi)(a-bi)

Therefore, 3 is prime in Z[i].

4n+3 is Gaussian primes such as 3,7,11,19,23,31,43,47,59,67,71,79,83. This is in Y^2=X^3-X.

E(N)=G(p)≒4n+3≠(a+bi)(a-bi)

E(N) is the sum of the same modules in Y^2=X^3-X. G(p) is Gaussian primes.



You see COUNTIF(mod(y^2),mod(x^3-x)) which is p=N.

---

python

Bernoulli distribution

We are back to civilized society, but this is heads or tails. This is gambling like stock market. The average line is 50%, so you have two choices which are up or down.

1 is head. 0 is tail.

P is probability.

If you have a die, probability of 1 is 1/6.

P(X=1)=1/6

0 is the other.

∴

P(X=0)=5/6

You have dice 10 times, and you get one 6 times.

P(X=6)=10C6*(1/6)^6*(5/6)^(10-6)≒0.2170635%

This is how many times you have 1 in 10 times.

---

dice

---

---

-

Binomial theorem

Orientalism is no formula. It is often mysticism of numbers. We can see algorism, but nobody knows where it comes from. Chinese blocks such as 一、二、三 are well known. Constructors gather and pile them. You still see their temples. Wood is vanishing ironically.

Polynomial keeps expanding, but there is a pattern. You keep adding numbers infinitely. We often see it naturally in the modern age.

x+y=1C0*x^0*y+1C1*x*y^0=x+y

(x+y)^2=2C0*x^0*y^2+2C1*x*y+2C2*x^2*y^0=x^2+2xy+y^2

(x+y)^3=3C0*x^0*y^3+3C1*x*y^2+3C2*x^2*y+3C3*x^3*y^0=x^3+3x*y^2+3x^2*y+y^3

(x+y)^4=4C0*x^0*y^4+4C1*x*y^3+4C2*x^2*y^2+4C3*x^3*y+4C4*x^4*y^0=x^4+4x*y^3+6x^2*y^2+4x^3*y+y^4

1	1
1	2	1
1	3	3	1
1	4	6	4	1

We know that this is convergence.

Pascal's triangle

I am a Japanese, so I am interested in mysterious something. AI still don't understand our consciousness. Future is uncertain, so you may change it. I am not so curious about it.

It is hard to read this Chinese character, but I try to translate it.

---

B0
B0*2C0
B0*3C0+B1*3C1
B0*4C0+B1*4C1+B2*4C2
B0*5C0+B1*5C1+B2*5C2+B3*5C3
B0*6C0+B1*6C1+B2*6C2+B3*6C3+B4*6C4
B0*7C0+B1*7C1+B2*7C2+B3*7C3+B4*7C4+B5*7C5

1
1	3
1	4	6
1	5	10	10
1	6	15	20	15
1	7	21	35	35	21
B0	B1	B2	B3	B4	B5

B0=1, B1=-1/2 but 1/2, B2=1/6, B3=0, B4=-1/30, B5=0

---

Now I see Bernoulli numbers in the Samurai era, although the country has been closed except for Holland and Portugal. We never know it in those days. Some Europeans may have taught us.

B6=1/42.

I clearly see it.

We don't understand the reason, but it seems to be Pascal's triangle.

N=6 and K=4

5C3=10

Then this samurai multiplies Bernoulli numbers apparently.

You sum the line between 1 and 0.

EX.
3/2+1/2=2
2+1=3
5/2+5/3-1/6=4
3+5/2-1/2=5
7/2+7/2-7/6+1/6=6
4+14/3-7/3+2/3=7
9/2+6-21/5+2-3/10=8
5+15/2-7+5-3/2=9
11/2+55/6-11+11-11/2+5/6=10
6+11-33/2+22-33/2+5=11

You get 1 to 11.

This is compression, and I try to find B12.

(13/2)+13+0-(143/6)+0+(286/7)+0-(429/10)+0+(65/3)+0+13B12=12

B12=-691/2730

Bernoulli number

Bernoulli numbers are almost the sum of k power.
Bn is the Bernoulli number. This is recurrence relation, so you change the direction back and forth.

You can also write this.

This is Maclaurin's expansion.
Then you can see this.

f(x)*(1/f(x))=1

This is convergence.

∴

from (2)

This is Binomial Coefficient.

∴

EX.
B0=1
B1=-1/2*(2C0)*B0=(-1/2)*1*1=-1/2
B2=-1/3*(3C0*B0+3C1B1)=(-1/3)*(-1/2)=1/6
B3=-1/4*(4C0*B0+4C1*B1+4C2*B2)=-1/4*(1-2+1)=0
B4=-1/5*(5C0*B0+5C1*B1+5C2*B2+5C3*B3)=(-1/5)*(1/6)=-1/30

All Bernoulli number is rational.
Bn is related to Riemann zeta function.

n→∞