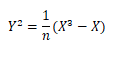Congruent number problem

Congruent number problem is Pythagorean theorem in elliptic curves which are rational number. You see that half of rectangular is in it. However, n=1 in Y^2=X^3-X. This is not congruent number.

This is algebra.

(n=5,6,7,13,14,15,20,95)

This is the same process with Y^2=X^3-X but the different elliptic curve. This is still fractal. n=5 is the first congruent number. n is the integer without square factors.

You can also write this. n is Congruent number.

ab/2=n

(a/c)^2+(b/c)^2=1

This is rational.
a=cx, b=cy

You remember rational point in X^2+y^2=1.

This is expansion, but you select proper numbers.

(n=5,6,7,13,14,15,20,95)

You see the horizon which is 0.

Y^2=X^3-n^2X
(n=157)

Elliptic curve

Is really rational number in an elliptic curve? This is the big question about complicated geometry, and it is very hard to capture it. We use prime numbers as modulo to avoid it. I think that it is fractal.

You see the circle.

x^2+y^2=1

a/c and b/c are rational.

(a/c)^2+(b/c)^2=1

x=a/c, y=b/c

∴

a=cx, b=cy

(1/2)ab=1

This is half of rectangular ab.

a^2+b^2=c^2

(3,4,5) is Congruent number which is rational, but 1 is not.
if ab=2, a=1 and b=2. c is irrational.
This is contradictory.

(1/2)cx*cy=(1/2)c^2*xy=1

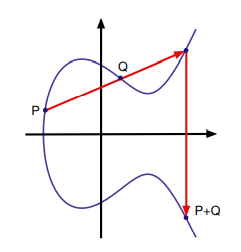
You see the rational point P.

You put P on x and y.

Then you get an elliptic curve.

Y^2=X^3-X

You use modulo.

For example, you see modulo 3.
You get x=(0,1,2) because 3 is 0 in modulo. You put it in y^2. y^2=(0,1,4)=(0,1,1) in modulo. Then, x^3-x=(0,0,6)=(0,0,0) in modulo.
You compare y^2 and x^3-x in modulo. You get (0,1,1) and (0,0,0). You see 0 in both side. x=(0,1,2) and y=(0,0,0)
You have 3 in y. This is prime number.

You repeat it over and over again. The sum of y is sometime prime, but you always have prime as modulo. 0 is hopeless but it is only solution according to Fermat.

The Birch and Swinnerton-Dyer Conjecture

This is the Birch and Swinnerton-Dyer Conjecture. Np is the number of points on E which is an elliptic curve over Q. 【mod p】 is on E, and p is a prime. If the rank of E is large then on average E should have more than p points. This is X. c is constant.

Q is rational numbers.

At first, you see a circle. X^2+y^2=1

P is a rational point. You have a line (-1,0) to P. s is a slope.

Y=s(X+1)

Then you put the line to X^2+y^2=1.

(s^2+1)X^2+(2s^2)X+(s^2-1)=0

∴ X=-1, (1-s^2)/(1+s^2)

You see P on the line.

P is a rational point on π, so it is infinite.

Q∪｛∞｝

If f(X,Y)=0, you pile circles and you have the point of infinity.

C is complex plane. P(C) is Riemann sphere.

This is the point of infinity. This cone is the three dimensions. This is quite complicated because of no rational point. Then you use an elliptic curve.

You can ignore zero.

P and Q are rational points, so P+Q on E is still rational even if P+Q is the point of infinity.

T is some finite abelian group.