Congruent number problem

Congruent number problem is Pythagorean theorem in elliptic curves which are rational number. You see that half of rectangular is in it. However, n=1 in Y^2=X^3-X. This is not congruent number.
This is algebra.
(n=5,6,7,13,14,15,20,95)

This is the same process with Y^2=X^3-X but the different elliptic curve. This is still fractal. n=5 is the first congruent number. n is the integer without square factors.

You can also write this. n is Congruent number.

ab/2=n


(a/c)^2+(b/c)^2=1


This is rational.
a=cx, b=cy
You remember rational point in X^2+y^2=1.
This is expansion, but you select proper numbers.
(n=5,6,7,13,14,15,20,95)

You see the horizon which is 0.
Y^2=X^3-n^2X
(n=157)

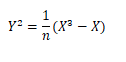
コメント

コメントを投稿

このブログの人気の投稿

The Sylvester-Gallai Theorem

イメージ
The deformation is the mathematical concept. The Sylvester-Gallai Theorem is that a finite set of points in the plane have the proper line through any two of them, and it passes through a third point of the set. Moreover, it must be on the same line. P is the the noncollinear finite set. S(P) is the set of connecting lines in P. p∈P, s∈S(P) p and s are perpendicular, so they are not the ordinary line. (s*,p*) is the smallest distance, and s* is in the ordinary line. l∩P={p} l must be the ordinary line. This is the contradiction. l∩S(P) There is the cyclically intersection points (p,x1). x1,・・・xk is on l. Moreover it crosses S. This must be ordinary. You also see the extra dimensions. i lines are determined by P.
続きを読む

Montgomery's pair correlation conjecture

イメージ
Hybrid orbitals are the explanation of molecular geometry and atomic bonding. This is Montgomery's pair correlation conjecture, which is the pair correlation between pairs of zeros of the Riemann zeta function . γ and　γ' are imaginary. This is like piling prime numbers . Methane and hydrogen are gasses. C=C is carbon bonding which is in surface. Gasses move like ↑ ↑ ↓. This is called π bond.
続きを読む

Hybrid orbital

イメージ
P^2+Σ2P is the pattern of prime numbers which move like atom. This is Carbon. There are 6 electrons. Σ is hybrid, and atomic orbitals are mixtures. Then, you see sp^3. You move one electron in 2S to 2P. This is called promotion. 2S lose one electron. There are 4 hydrogen atoms. This is tetrahedron and sp^3. Methane is CH4. In sp^2 hybridisation, 2S move to 2P. This is triangle and sp^2.　Ethylen is C2H4 which is the double bond. C=C is connected tightly.
続きを読む